[TOC]

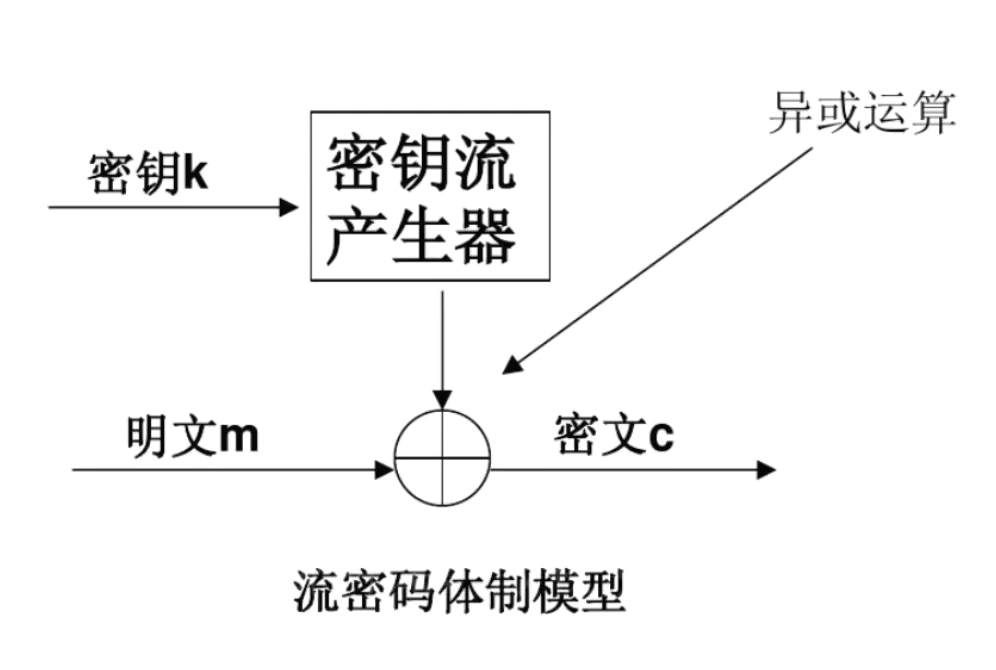
序列密码(流密码) ¶

将明文消息按字符逐位进行加密。

stream_cipher

RC4 ¶

RC4(Rivest Cipher 4)是一种流加密算法，密钥长度可变。在给定一密钥时，会生成一固定序列的字节流，用于和明文进行异或。

用途：WEP、WPA、SSL、TLS

原理 ¶

RSA主要包括初始化算法(KSA)和伪随机子密码生成算法(PRGA)，其核心部分的S-box长度可为任意，但一般为256字节。

RC4算法的关键是根据明文和密钥生成相应的密钥流，密钥流长度和明文长度相等，密文[i] = 明文[i] ^ 密钥流[i]

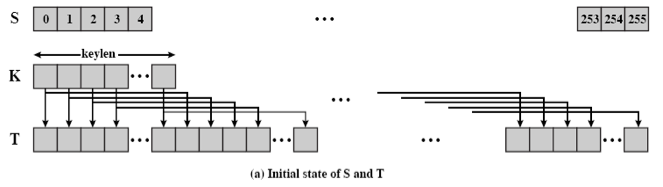
初始化算法(KSA) ¶

初始化存储0-255字节的S-box和T-box

填充key到256个字节数组中称为T-box，（key不满256则循环填充、超过则只取前256）
1
2
3
4
5
N = 256;
for (i=0;i < N;i++) {
S[i] = i;
T[i] = key[i % key_len];
}

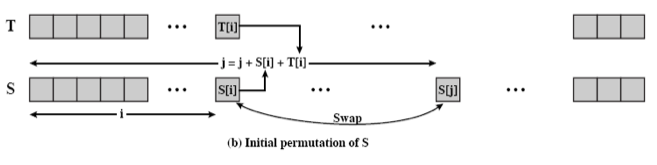
初始置换状态向量S-box

N = 256;
for (i=0, j=0; i< N; i++)
{
	j=(j+S[i]+T[i])% N;
    // 对两数进行交换
	swap(S[i], S[j]);
}

伪随机子密码生成算法(PRGA) ¶

产生密钥流，并与明文异或得到密文

i=0;
j=0;
for (k = 0; k < data_len; k++) {
    i = (i + 1) % 256;
    j = (j + S[i]) % 256;
    
    tmp = S[i];
    S[i] = S[j]; //交换S[x]和S[y]
    S[j] = tmp;
    
    t = (S[i] + S[j]) % 256;
    ckey = S[t];	// ckey为生成的密钥流
    data[k] ^= ckey;
}

实现 ¶

C语言 ¶

分组密码(块加密) ¶

将明文消息分组(每组多个字符)，逐组进行加密。

分组密码概念 ¶

padding，即 padding(填补) 到指定分组长度。
分组加密工作模式，即明文分组加密的方式。

分组密码最后不足一个区块的大小，称为短块，短块的处理方法有填充法、流密码加密法、密文挪用技术。

分组密码五种工作模式 ¶

DES算法工作模式被标准化，根据数据加密时每个加密区块间的关联方式来区分，可以分为以下4种：

电子密码本模式(Electronic Code Book, ECB)
密文链接模式(Cipher Book Chaining, CBC)
密文反馈模式(Cipher Feed Back, CFB)
输出反馈模式(Output Feed Back, OFB)
（AES标准额外添加一种）计数器模式(Counter, CTR)

这些工作模式可适用于各种分组密码算法

模式	描述	使用途径
ECB（电码本模式）	用于每一个明文组独立的用同一密钥加密	传送短数据 ( 如一个加密密钥）
CBC（密码分组链接模式）	加密算法的输入是当前明文组与前一密文组的异或	传送数据分组；认证
CFB（密码反馈模式）	每次只处理输入的 j 比特 , 将上一次的密文用作加密算法的输入以产生伪随机输出 , 该输出再与当前明文异或以产生当前密文	传送数据分组；认证
OFB（输出反馈模式）	与 CFB 类似 ,不同之处是本次加密算法的输入为前一次加密算法的输出	有扰信道传送数据
CTR (计数器模式)	与CFB、OFB些许类似，但不同之处是定义一个计数器来加密后进行异或

电子密码本模式(ECB) ¶

ECB图解

ECB是最简单的运行模式，它一次对一个64bit的明文分组利用相同的密钥进行加密，当密钥取定时，对明文的每一个分组，都有一个惟一的密文与之对应。如果消息长于64比特,则将其分为长为64比特的分组，最后一个分组如果不够64bit，则需要对这个分组进行填充。解密过程也是一次对一个分组解密，而且每次解密都使用同一密钥。

每次加密均产生独立的密文分组，每组的加密结果不会对其他分组差生影响，相同的明文加密后对应产生相同的密文，无初始化向量(加密向量,iv)

优点：简单易行，便于实现并行操作，没有误差传递的问题
缺点：不能隐藏明文的模式，如果同一明文重复出现、密文也会重复，密文内容很容易被替换、重排、删除、重放；对明文进行主动攻击的可能性较高
用途：适合加密密钥，随机数等短数据。

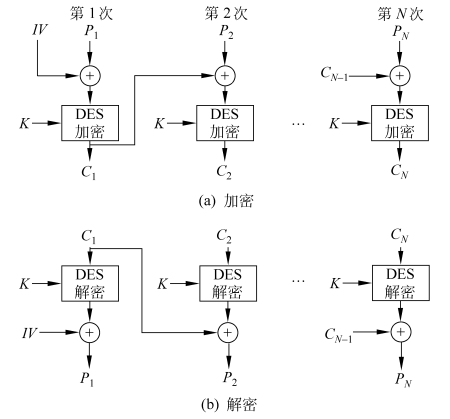
密文链接模式(CBC) ¶

⊕表示异或

CBC图解

为了解决ECB模式的密文块相同的缺点，CBC的模式引入了一个初始向量概念(IV)。在第一次加密前，会使用初始化向量与第一个明文分组异或，生成的数据分组再进行加密；加密第二个分组之前，会拿第一块的密文数据与第二个明文分组进行异或运算后再进行加密，以此类推，解密时也是在解密后，再与前一分组进行异或运算，生成最终的明文。

优点：CBC加密后密文上下文关联，即使明文出现重复信息也不会产生相同密文；密文内容如果被替换重排删除重放或传输错误，后续密文即被破坏，无法完成解密还原。
缺点：不利于并行计算；误差传递；需要初始化向量(IV)
用途：可加密任意长度的数据，适用于计算产生检测数据完整性的消息认证码MAC

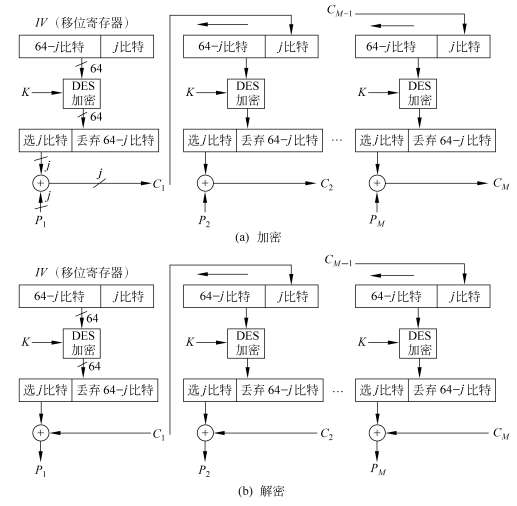
密码反馈模式(CFB) ¶

利用CFB或者OFB模式，可将DES转换为流密码。它可以按字节逐个进行加密解密，也可以按照n位字节处理。

设传送的每个单元(如一个字符)长度是j比特(通常取8bit)，与CBC一样，明文单元被链接到一起，使得密文是前面所有明文的函数

CFB图解

加密时，加密算法的输入是64比特移位寄存器，初值为某个初始向量IV。加密算法输出的最左(最高有效位) j 比特与明文的第一个单元P₁异或，产生出的密文的第一个单元C₁，并传送该单元。然后将移位寄存器的内容左移 j 位，并将C₁送入送入移位寄存器最右边(最低有效位) j 位。这一过程继续到明文所有单元都被加密为止。

通俗解释，看图，首先j比特为加密的单元长度，初次的移位寄存器为IV，先将其进行DES加密，之后选取左侧的j比特与明文的第一个单元P₁进行异或，之后将原先的IV左移j位(抛弃运算完成的j位)，然后将P₁异或结果C₁( j 比特) 填补到移位寄存器的右侧(最低有效位) j 位，并开始下一次的加密、异或。

解密时，将受到的密文单元与加密函数的输出进行异或。

优点：隐藏了明文的模式，每个分组加密结果必受前面所有分组内容的影响，多次相同明文均产生不同密文；分组密码转化为流模式，可产生密钥流；可及时加密传送小于分组的数据。
缺点：不利于并行计算；存在误差传送；需要初始化向量。
用途：因错误传播无界，可用于检查发现明文密文的篡改。

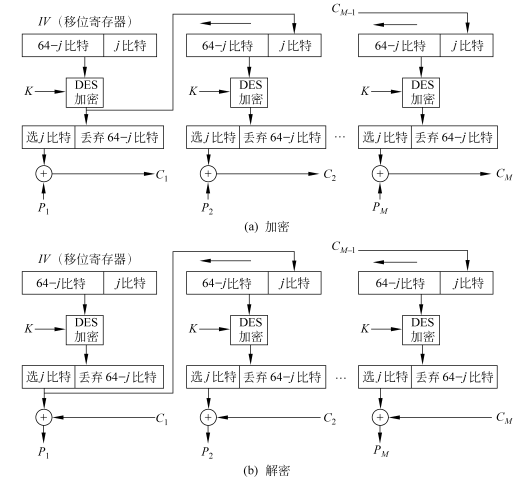
输出反馈模式(OFB) ¶

OFB模式的结构类似于CFB，不同之处在于：OFB是将加密算法的输出反馈到移位寄存器，而CFB则是将密文单元反馈到移位寄存器。

OFB图解

优点：传输过程中的比特错误不会被传播、后各明文单元不受影响（无误差传送问题）；
缺点：不利于并行运算，比CFB模式更易受到对消息流的篡改攻击。
用途：适用于加密冗余性较大的数据，如语音和图像数据。

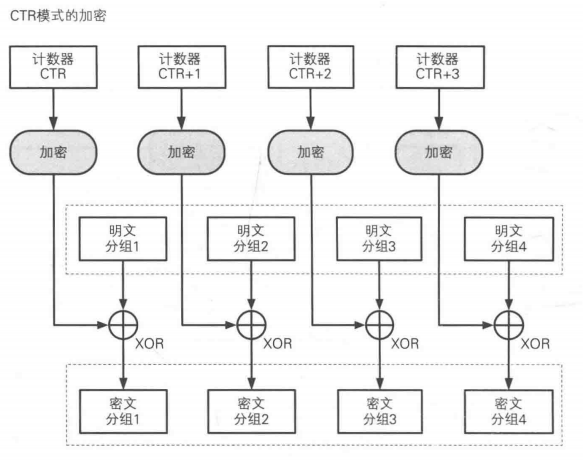
计数器模式(CTR) ¶

CTR模式（Counter mode，CM）也被称为ICM模式（Integer Counter Mode，整数计数模式）和SIC模式（Segmented Integer Counter），与OFB相似，CTR将块密码变为流密码。它通过递增一个加密计数器以产生连续的密钥流，其中，计数器可以是任意保证长时间不产生重复输出的函数，但使用一个普通的计数器是最简单和最常见的做法。

加密：通过对逐次累加的计数器加密来生成密钥分组，与明文分组异或产生密文分组。

解密：同加密。

CTR图解

**例如：**AES-128，首先选择一个IV（长度小于分组长度，比如96位），而剩下的32位则由计数器使用，并且该CTR值初始化为0。在会话期间加密的每个分组，计数器都会递增而IV则保持不变。

优点：可并行计算

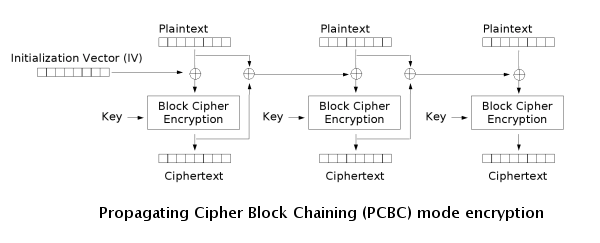
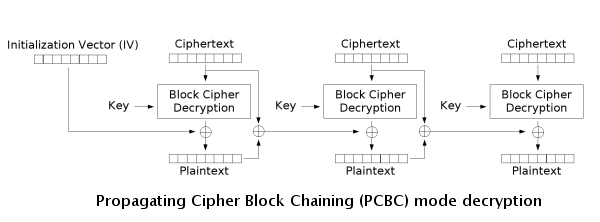
明文密码块链接(PCBC) ¶

PCBC 的全称为明文密码块链接（Plaintext cipher-block chaining）。也称为填充密码块链接（Propagating cipher-block chaining）。

加密

pcbc_encryption

解密

pcbc_decryption

分组密码填充模式 ¶

需要注意的是，即使消息的长度是块大小的整数倍，仍然需要填充。（其它填充规则）

NoPadding ¶

不填充，在此填充下原始数据必须是分组大小的整数倍，非整数倍时无法使用该模式

PKCS5Padding / PKCS7Padding ¶

填充至符合块大小的整数倍，填充值为[填充数量数]

原始：FF FF FF FF FF FF FF FF FF (9 byte)
填充：FF FF FF FF FF FF FF FF FF 07 07 07 07 07 07 07 (假设填充至16byte，需7byte，则填充值为07)

特殊情况：PKCS#7规定Padding必须存在，因此即使原始数据是16的整数倍，也需要在末尾追加16字节的Padding，即正好追加一个块，这个块每个字节都是0x10

PKCS5Padding 的分组大小固定为 8 个字节，而 PKCS7Padding 的分组大小可以在 1~255 字节。但 SunJCE 的 Provider 实现中 PKCS5Padding 也按 PKCS7Padding 来进行处理了（因为AES并没有64位的块, 如果采用PKCS5, 那么实质上就是采用PKCS7）。

ANSI X923Padding ¶

填充至符合块大小的整数倍，填充值最后一个字节为[填充数量数]，其他字节填 00

原始：FF FF FF FF FF FF FF FF FF
填充：FF FF FF FF FF FF FF FF FF 00 00 00 00 00 00 07

特殊情况：只有一个字节填充，则直接填充01(填充数量)

ISO10126Padding ¶

填充至符合块大小的整数倍，填充值最后一个字节为[填充数量数]，其他字节随机处理

原始：FF FF FF FF FF FF FF FF FF
填充：FF FF FF FF FF FF FF FF FF 3F 7A B4 09 14 36 07 (填充7byte，最后填充值为07，其余填充随机)

特殊情况：只有一个字节填充，则直接填充01(填充数量)

ISO7816-4Padding ¶

填充至符合块大小的整数倍，填充值第一个字节为 0x80，其他字节填 00

原始：FF FF FF FF FF FF FF FF FF
填充：FF FF FF FF FF FF FF FF FF 80 00 00 00 00 00 00

ZeroBytePadding ¶

填充至符合块大小的整数倍，填充值为 0

原始：FF FF FF FF FF FF FF FF FF
填充：FF FF FF FF FF FF FF FF FF 00 00 00 00 00 00 00

TBCPadding（Trailing-Bit-Compliment） ¶

填充至符合块大小的整数倍，原文最后一个bit位为1时填充 00，最后一位为0时填充FF

原始：FF FF FF FF FF FF FF FF FF
填充：FF FF FF FF FF FF FF FF FF 00 00 00 00 00 00 00
原始：FF FF FF FF FF FF FF FF F0
填充：FF FF FF FF FF FF FF FF F0 FF FF FF FF FF FF FF

PKCS1Padding ¶

该填充模式是 RSA 加密中使用的，详见 RFC 2313 - PKCS #1: RSA Encryption Version 1.5 (ietf.org)。

要求：必须比RSA钥模长(modulus)短至少11byte，也就是RSA_size(rsa) - 11，输出和modulus一样长

例如：密钥长度为1024位(bit)，则输出的密文块长度为128byte，输入的明文块长度则为128-11 = 117byte；如果明文过长、需要切割；明文较短、需要填充，填充规则如下

RSA 加密时，需要将原文填充至密钥大小，加密块是一个8位字节串EB，它由块标记BT 、填充块PS、原数据D组成：EB = 00 | BT | PS | 00 | D

00 为固定字节
BT 为处理模式。私钥操作为 00 或 01，公钥操作时为 02
PS 为填充字节块，填充数量为 k - 3 - D(减去的3即为00|BT|00)，k 表示密钥长度，D 表示原文长度。PS 的最小长度为 8 个字节。填充的值根据 BT 值不同而不同：
- BT = 00 时，填充全 00
- BT = 01 时，填充全 FF
- BT = 02 时，随机填充，但不能为 00
D 为填充前原文

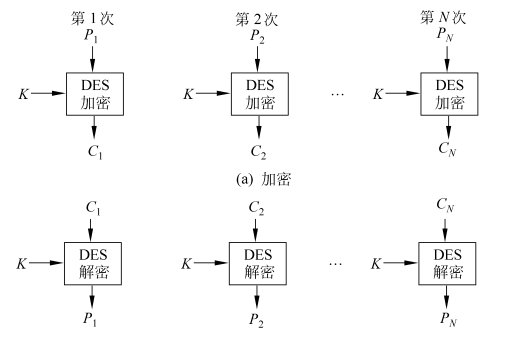
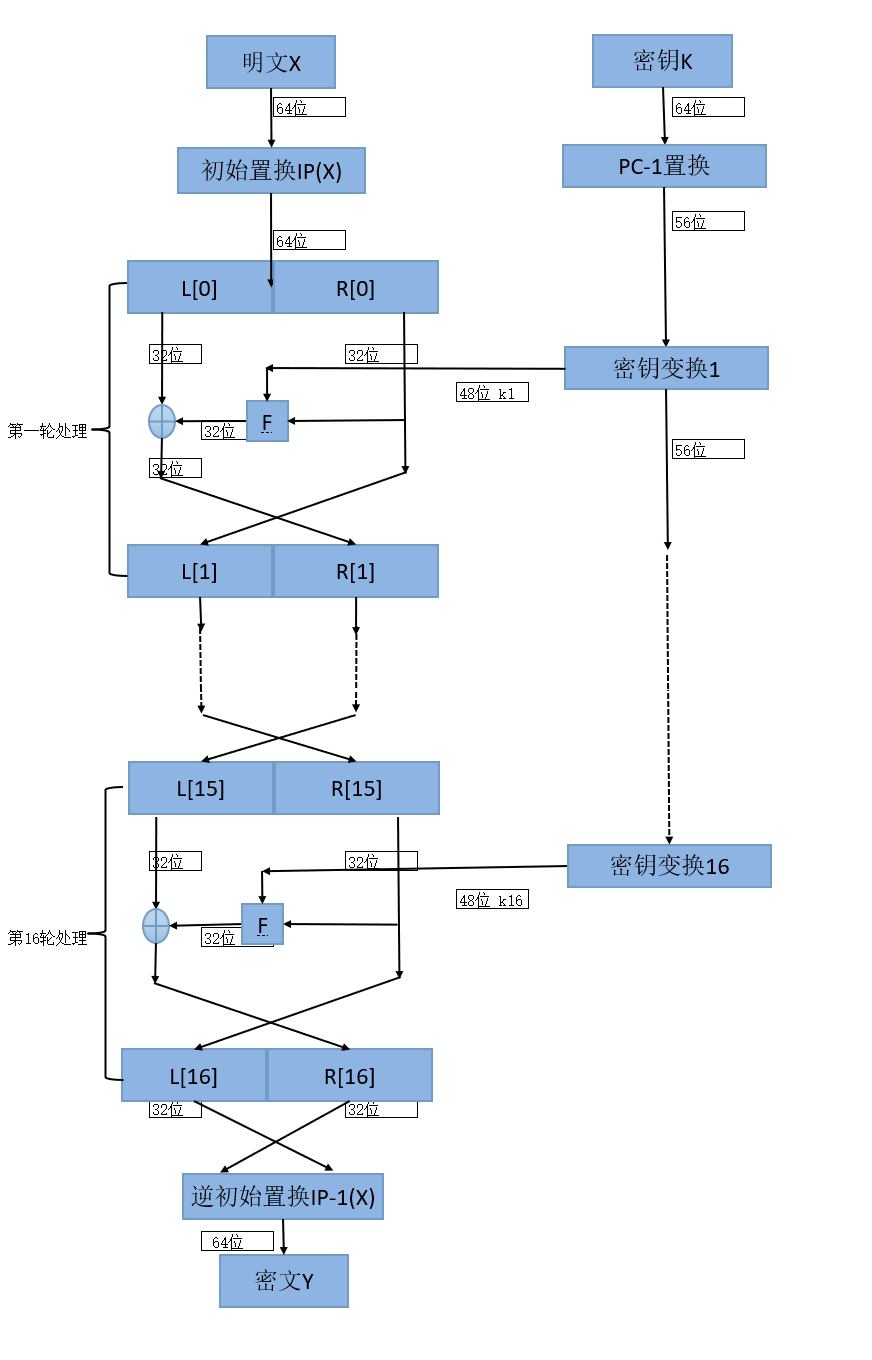
DES ¶

分组加密算法：以64位为分组。64位明文输入，64位密文输出
对称算法：加密和解密使用同一秘钥。
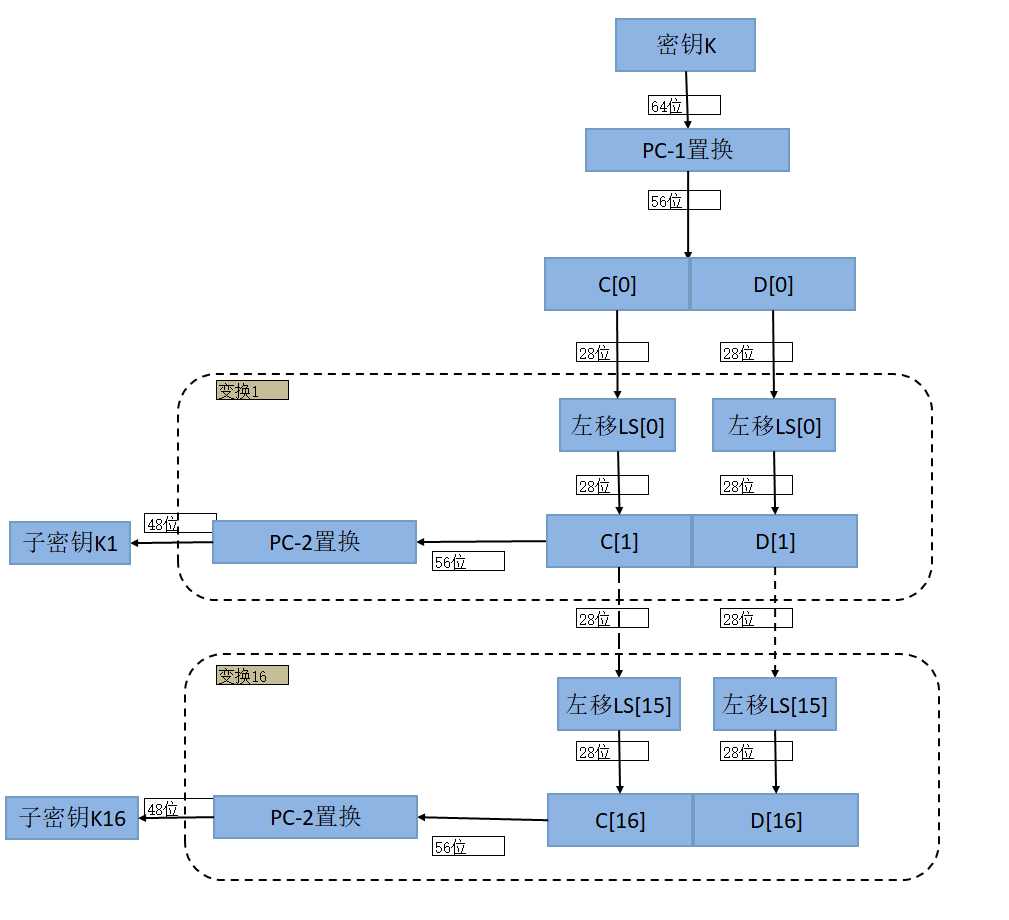
密钥 64 位，使用 64 位密钥中的 56 位，剩余的 8 位要么丢弃，要么作为奇偶校验位(第8、16、24、32、40、48、56、64作为校验位)。
Feistel 迭代结构
- 明文经过 16 轮迭代得到密文。
- 密文经过类似的 16 轮迭代得到明文。

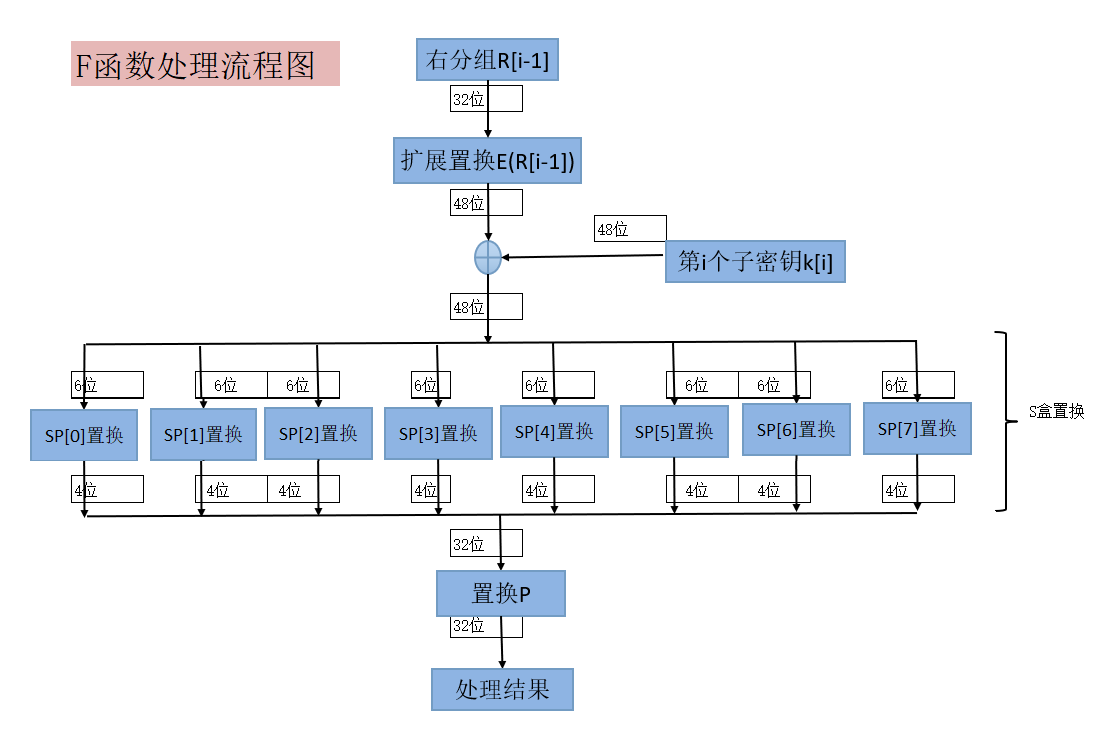
原理 ¶

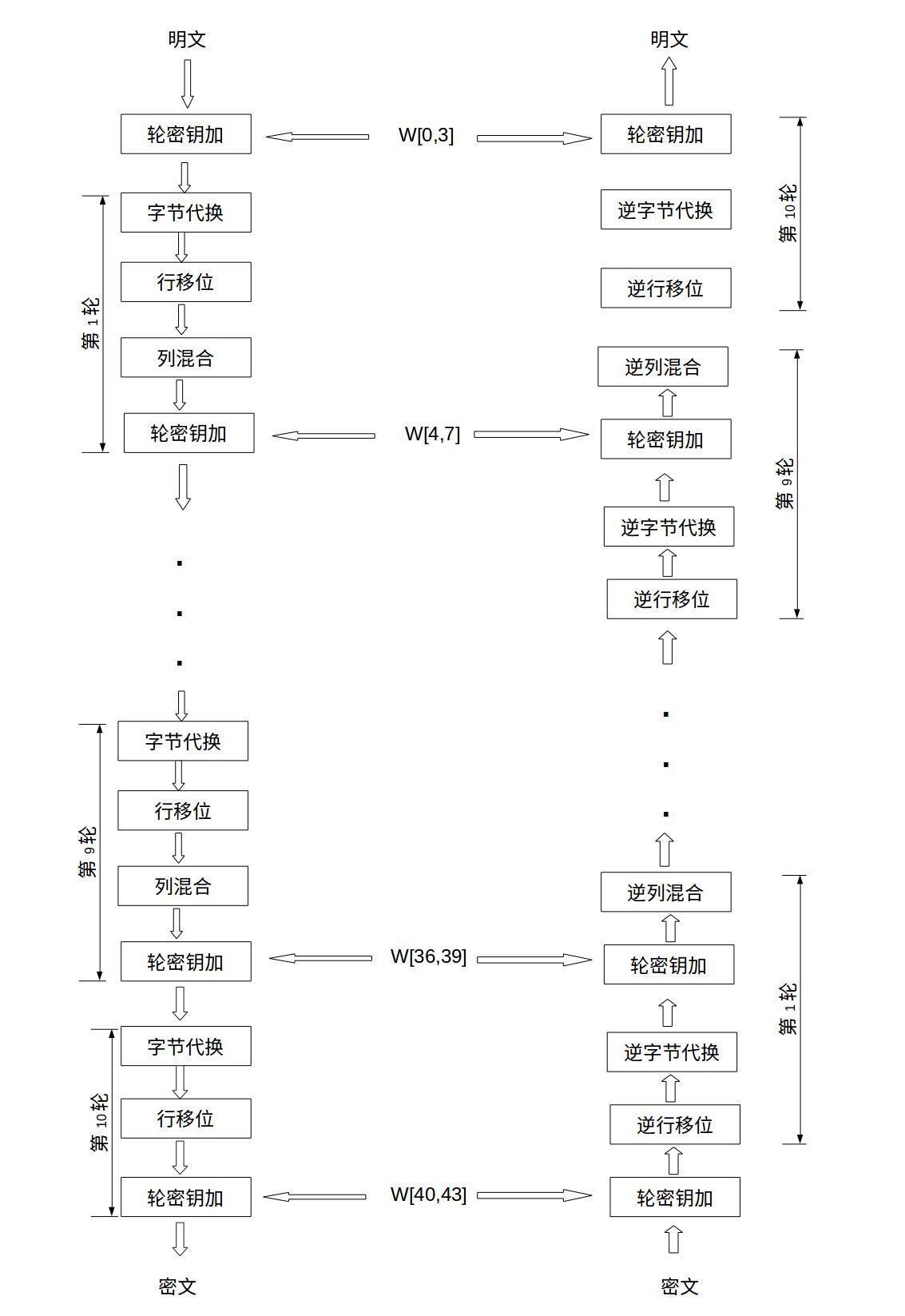
大致图

DES-0

F函数

DES-1

密钥生成图

DES-2

实现 ¶

Java ¶

DESede(3DES) ¶

DESede同时又可称为3DES(三重DES)或TripleDES

三重 DES 的加解密方式如下

$C=E_{k3}(D_{k2}(E_{k1}(P)))$

$P=D_{k1}(E_{k2}(D_{k3}(C)))$

在选择密钥时，可以有两种方法

3 个不同的密钥，k1，k2，k3 互相独立，一共 168 比特。
2 个不同的密钥，k1 与 k2 独立，k3=k1，112 比特。

当三个密钥均相同时，此时与DES加密无异

实现 ¶

Java ¶

在Java中，传入的key字节数组需满足length==18，也就是原DES的key的三个，至于key的选取规则，则留给用户遵守

/**
 * DESede ECB 模式加密
 *
 * @param data 需要加密的数据字符串
 * @param key  加密的key
 */
public static String des3ECBcrypt(byte[] data, byte[] key) {
    // 加密结果字节数组
    byte[] encrypted;
    // 加密结果字符串
    String result = null;
    if (null != key && key.length != 24) {
        System.out.println("DESede uses a key length of 24 bytes (192 bits).");
        return result;
    }
    try {
        // 实例化 密钥材料
        DESedeKeySpec desKey = new DESedeKeySpec(key);
        // 实例化 密钥生成器
        SecretKeyFactory keyFactory = SecretKeyFactory.getInstance("DESede");
        // 生成密钥
        SecretKey secretKey = keyFactory.generateSecret(desKey);


        // 指定加密模式 实例化Ciper对象
        Cipher cipher = Cipher.getInstance("DESede/ECB/PKCS5Padding"); // 加密方式/工作模式/填充模式
        // 初始化,设置加密(1)或解密(2)
        cipher.init(Cipher.ENCRYPT_MODE, secretKey);
        // 执行，得到结果字节数组
        encrypted = cipher.doFinal(data);
        // 对结果字节数组进行base64编码，得到加密后的字符串
        result = Base64.getEncoder().encodeToString(encrypted);
    } catch (InvalidKeyException | NoSuchAlgorithmException | NoSuchPaddingException | BadPaddingException | IllegalBlockSizeException | InvalidKeySpecException e) {
        e.printStackTrace();
    }
    return result;
}

其实就是相比DES，将DESKeySpec类替换为DESedeKeySpec类，将字符串DES替换为DESede

调用

System.out.println(des3ECBcrypt("Forgo7ten".getBytes(StandardCharsets.UTF_8), "123456781234567812345678".getBytes(StandardCharsets.UTF_8)));	// 由于三个key相同，则加密结果与一个key的DES结果相同

AES ¶

AES	密钥长度(32位比特字)	分组长度(32位比特字)	加密轮数
AES-128	4(128位)	4	10
AES-192	6	4	12
AES-256	8	4	14

原理 ¶

AES算法是对称密码，主要有四种操作处理，分别是密钥加法层(也叫轮密钥加，英文Add Round Key)、字节代换层(SubByte)、行位移层(Shift Rows)、列混淆层(Mix Column)。

而明文x和密钥k都是由16个字节组成的数据(当然密钥还支持192位和256位的长度，暂时不考虑)，它是按照字节的先后顺序从上到下、从左到右进行排列的。

AES算法在处理的轮数上只有最后一轮操作与前面的轮处理上有些许不同(最后一轮只是少了列混淆处理)，在轮处理开始前还单独进行了一次轮密钥加的处理。在处理轮数上，我们只考虑128位密钥的10轮处理。

AES-0

字节代换操作 ¶

状态矩阵中的元素按照下面的方式映射为一个新的字节：

把该字节的高4位作为行值，低4位作为列值，取出S盒或者逆S盒中对应的行的元素作为输出。

例如，加密时，输出的字节S1为0x12,则查S盒的第0x01行和0x02列，得到值0xc9,然后替换S1原有的0x12为0xc9。

S盒为16*16

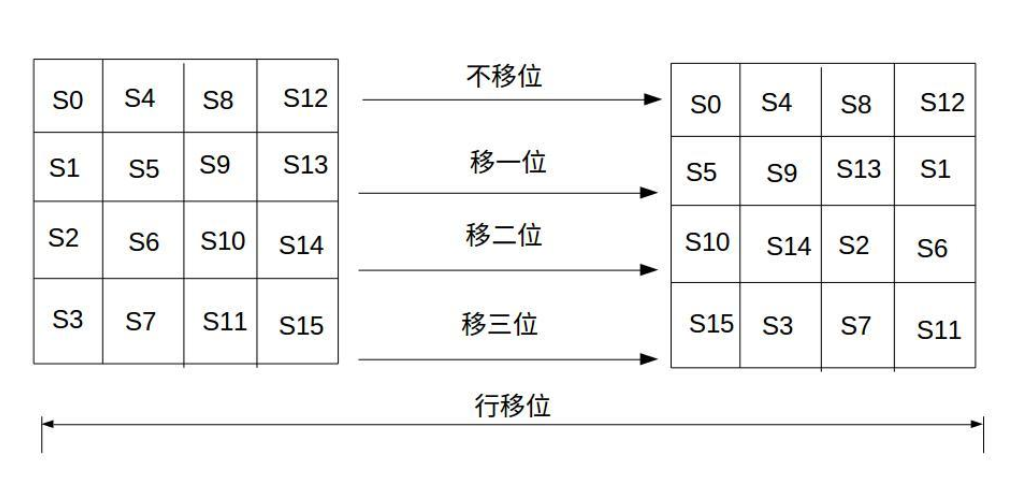
行位移操作 ¶

行移位是一个简单的左循环移位操作。

AES-1-行位移加密

当密钥长度为128比特时，在加密时，保持矩阵的第一行不变，第二行向左移动8Bit(一个字节)、第三行向左移动2个字节、第四行向左移动3个字节。而在解密时恰恰相反，依然保持第一行不变，将第二行向右移动一个字节、第三行右移2个字节、第四行右移3个字节。

列混淆 ¶

列混合变换是通过矩阵相乘来实现的，经行移位后的状态矩阵与固定的矩阵相乘，得到混淆后的状态矩阵

实现 ¶

Java ¶

TEA系列密码 ¶

SM4算法 ¶

SM4算法的特征 ¶

S盒固定

unsigned char TAO[16][16] =
{
    {0xd6,0x90,0xe9,0xfe,0xcc,0xe1,0x3d,0xb7,0x16,0xb6,0x14,0xc2,0x28,0xfb,0x2c,0x05},
    {0x2b,0x67,0x9a,0x76,0x2a,0xbe,0x04,0xc3,0xaa,0x44,0x13,0x26,0x49,0x86,0x06,0x99},
    {0x9c,0x42,0x50,0xf4,0x91,0xef,0x98,0x7a,0x33,0x54,0x0b,0x43,0xed,0xcf,0xac,0x62},
    {0xe4,0xb3,0x1c,0xa9,0xc9,0x08,0xe8,0x95,0x80,0xdf,0x94,0xfa,0x75,0x8f,0x3f,0xa6},
    {0x47,0x07,0xa7,0xfc,0xf3,0x73,0x17,0xba,0x83,0x59,0x3c,0x19,0xe6,0x85,0x4f,0xa8},
    {0x68,0x6b,0x81,0xb2,0x71,0x64,0xda,0x8b,0xf8,0xeb,0x0f,0x4b,0x70,0x56,0x9d,0x35},
    {0x1e,0x24,0x0e,0x5e,0x63,0x58,0xd1,0xa2,0x25,0x22,0x7c,0x3b,0x01,0x21,0x78,0x87},
    {0xd4,0x00,0x46,0x57,0x9f,0xd3,0x27,0x52,0x4c,0x36,0x02,0xe7,0xa0,0xc4,0xc8,0x9e},
    {0xea,0xbf,0x8a,0xd2,0x40,0xc7,0x38,0xb5,0xa3,0xf7,0xf2,0xce,0xf9,0x61,0x15,0xa1},
    {0xe0,0xae,0x5d,0xa4,0x9b,0x34,0x1a,0x55,0xad,0x93,0x32,0x30,0xf5,0x8c,0xb1,0xe3},
    {0x1d,0xf6,0xe2,0x2e,0x82,0x66,0xca,0x60,0xc0,0x29,0x23,0xab,0x0d,0x53,0x4e,0x6f},
    {0xd5,0xdb,0x37,0x45,0xde,0xfd,0x8e,0x2f,0x03,0xff,0x6a,0x72,0x6d,0x6c,0x5b,0x51},
    {0x8d,0x1b,0xaf,0x92,0xbb,0xdd,0xbc,0x7f,0x11,0xd9,0x5c,0x41,0x1f,0x10,0x5a,0xd8},
    {0x0a,0xc1,0x31,0x88,0xa5,0xcd,0x7b,0xbd,0x2d,0x74,0xd0,0x12,0xb8,0xe5,0xb4,0xb0},
    {0x89,0x69,0x97,0x4a,0x0c,0x96,0x77,0x7e,0x65,0xb9,0xf1,0x09,0xc5,0x6e,0xc6,0x84},
    {0x18,0xf0,0x7d,0xec,0x3a,0xdc,0x4d,0x20,0x79,0xee,0x5f,0x3e,0xd7,0xcb,0x39,0x48}
};

系统参数 FK 固定

1	unsigned long FK[4] = {0xa3b1bac6, 0x56aa3350, 0x677d9197, 0xb27022dc};

固定参数 CK 固定

unsigned long CK[32] =
{
    0x00070e15, 0x1c232a31, 0x383f464d, 0x545b6269,
    0x70777e85, 0x8c939aa1, 0xa8afb6bd, 0xc4cbd2d9,
    0xe0e7eef5, 0xfc030a11, 0x181f262d, 0x343b4249,
    0x50575e65, 0x6c737a81, 0x888f969d, 0xa4abb2b9,
    0xc0c7ced5, 0xdce3eaf1, 0xf8ff060d, 0x141b2229,
    0x30373e45, 0x4c535a61, 0x686f767d, 0x848b9299,
    0xa0a7aeb5, 0xbcc3cad1, 0xd8dfe6ed, 0xf4fb0209,
    0x10171e25, 0x2c333a41, 0x484f565d, 0x646b7279
};

使用python库对SM4算法进行解密 ¶

标准128位加密

>>> from pysm4 import encrypt, decrypt
# 明文
>>> clear_num = 0x0123456789abcdeffedcba9876543210
# 密钥
>>> mk = 0x0123456789abcdeffedcba9876543210
# 加密
>>> cipher_num = encrypt(clear_num, mk)
>>> hex(cipher_num)[2:].replace('L', '')
'681edf34d206965e86b3e94f536e4246'
# 解密
>>> clear_num == decrypt(cipher_num, mk)
True

非对称密码 ¶

RSA ¶

基本原理 ¶

前置数学知识 ¶

互质关系 ¶

如果两个正整数，除了 $1$ 以外，没有其他公因子，我们就称这两个数是互质关系

不是质数也可以构成互质关系，比如 $15$ 和 $32$ 。
任意两个质数构成互质关系，比如 $13$ 和 $61$ 。
一个数是质数，另一个数只要不是前者的倍数，两者就构成互质关系，比如 $3$ 和 $10$ 。
如果两个数之中，较大的那个数是质数，则两者构成互质关系，比如 $97$ 和 $57$ 。
$1$ 和任意一个自然数是都是互质关系，比如 $1$ 和 $99$ 。
$p$ 是大于 $1$ 的整数，则 $p$ 和 $p-1$ 构成互质关系，比如 $57$ 和 $56$ 。
$p$ 是大于 $1$ 的奇数，则 $p$ 和 $p-2$ 构成互质关系，比如 $17$ 和 $15$ 。

欧拉函数 ¶

任意给定正整数 $n$ ，在小于等于 $n$ 的正整数之中，能与 $n$ 构成互质关系的数的个数；计算这个值的方法叫做欧拉函数，以 $\varphi (n)$ 表示。

如果 $n=1$ ，则 $\varphi(1) = 1$ 。因为1与任何数（包括自身）都构成互质关系
如果n是质数，则 $\varphi(1) = n-1$ 。因为质数与小于它的每一个数，都构成互质关系
如果n是质数的某一个次方，即 $n = p^k$ ( $p$ 为质数， $k$ 为大于等于 $1$ 的整数)，则 $\varphi(p^k) = p^k - p^{k-1}$ ；也可以写成 $\varphi(p^k)=p^k-p^{k-1}=p^k(1-\frac1p)$
如果n可以分解成两个互质的整数之积，即 $n = p1 \times p2$ ；则 $\varphi(n) = \varphi(p1 \times p2) = \varphi(p1) \times \varphi(p2)$ ，即积的欧拉函数等于各个因子的欧拉函数之积。

欧拉定理 ¶

如果两个正整数a和n互质，则n的欧拉函数 $\varphi (n)$ 可以让下面的等式成立：

$a^{\varphi(n)} \equiv 1\pmod n$

也就是说， $a$ 的 $\varphi(n)$ 次方除以 $n$ 的余数为1。

费马小定理：
假设正整数 $a$ 与质数 $p$ 互质，因为质数p的 $\varphi (p)$ 等于 $p-1$ ，则欧拉定理可以写成

$a^{p-1} \equiv 1\pmod p$

模反元素 ¶

如果两个正整数 $a$ 和 $n$ 互质，那么一定可以找到整数 $b$ ，使得 $ab-1$ 被 $n$ 整除，或者说 $ab$ 除以 $n$ 的余数是 $1$ 。
$ab \equiv 1\pmod n$
这时候b就叫做a的"模反元素"。

而 $a^{\varphi(n)}=a\times a^{\varphi(n)-1}\equiv 1\pmod n$ ，可以得到 $a^{\varphi(n)-1}$ 就是 $a$ 的模反元素。

公钥与私钥的产生 ¶

随机选择两个不相等大质数 $p$ 和 $q$ ，计算 $N = p \times q$
根据欧拉函数，求得 $N$ 的欧拉函数： $\varphi (N)=\varphi (p)\varphi (q)=(p-1)(q-1)$ [^rsa 公钥与私钥的产生-2]
选择一个小于 $\varphi (N)$ 的整数 $e$ （ $e$ 需满足 $1<e<\varphi (N)$ 且 $e$ 和 $\varphi (N)$ 互质；实际应用中，常常选择 $65537$ ）。并求得 $e$ 关于 $\varphi (N)$ 的模反元素，命名为 $d$ ，有 $ed\equiv 1 \pmod {\varphi (N)}$
将 $p$ 和 $q$ 的记录销毁

此时， $(N,e)$ 是公钥， $(N,d)$ 是私钥， $(N,e,d)$ 是密钥对。

[^rsa 公钥与私钥的产生-2]: 根据前置数学知识的欧拉函数[4]可知 $\varphi (N)=\varphi (p)\varphi (q)$ ，由[2]可知 $\varphi (p)\varphi (q)=(p-1)(q-1)$

产生的公钥和私钥均可用于加解密操作，用公钥加密的数据只能由对应的私钥解密，反之亦然。一般常用于以下两种途径：

私钥用于签名，公钥用于验签。
公钥用于加密、私钥用于解密。

消息加密 ¶

首先需要将消息以一个双方约定好的格式转化为一个小于 $N$ ，且与 $N$ 互质的整数 $m$ 。如果消息太长，可以将消息分为几段，这也就是我们所说的块加密，后对于每一部分利用如下公式加密：

$m^{e}\equiv c\pmod N$

消息解密 ¶

利用密钥 $d$ 进行解密。

$c^{d}\equiv m\pmod N$

举例 ¶

私钥公钥的产生 ¶

选择两个质数：选择 $61$ 和 $53$
计算pq的乘积n： $n = 61\times 53 = 3233$ ；n的长度就是密钥长度。3233写成二进制是110010100001，一共有12位，所以这个密钥就是12位。实际应用中，RSA密钥一般是1024位，重要场合则为2048位。
计算n的欧拉函数 $\varphi (n)$ $\varphi (3233) = (61-1)\times(53-1) = 60\times52 = 3120$
选取整数 $e$ ，选择为 $17$
计算e对于 $\varphi (n)$ 的模反元素d

也就是使得 $ed \equiv 1\pmod {\varphi(n)}$ 成立，等价于 $ed-1 = k\varphi(n)$

已知 $e=17$ ， $\varphi(n)=3120$ ，也就是 $17d+3120k = 1$ 成立，通过拓展欧几里得算法求得一组解为 $(d,k) = (2753,-15)$ ，即 $d=2753$
封装公钥和私钥

公钥为 $(n,e) = (3233, 17)$ ；私钥为 $(n,d) = (3233, 2753)$

破解 ¶

已知 $n$ 和 $e$ ，推导出 $d$

根据 $ed\equiv 1 \pmod {\varphi (N)}$ ：只有知道 $e$ 和$ \varphi (N) $，才能算出$ d$
而 $\varphi (N)=(p-1)(q-1)$ ：只有知道 $p$ 和 $q$ ，才能算出$ \varphi (N) $
而 $n=pq$ 。只有将 $n$ 因数分解，才能算出 $p$ 和 $q$

如果n可以被因数分解，d就可以算出，也就意味着私钥被破解。

实现 ¶

Java ¶

java的代码中的private key必须使用pkcs#8格式的

密钥格式：

PKCS#8：-----BEGIN PRIVATE KEY----- （JAVA格式）
PKCS#1：-----BEGIN RSA PRIVATE KEY----- （JAVA不支持）

学习更多

Java RSA私钥的格式pkcs1和pkcs8、PrivateKey转换_茅坤宝骏氹的博客-CSDN博客

工具 ¶

RSAtool ¶

安装

1
2
3

git clone https://github.com/ius/rsatool.git
cd rsatool
python rsatool.py -h

生成私钥

1	python rsatool.py -f PEM -o private.pem -p 1234567 -q 7654321

RSA Converter ¶

根据给定密钥对，生成 pem 文件
根据 nn，ee，dd 得出 pp，qq

openssl ¶

查看公钥文件

1	openssl rsa -pubin -in pubkey.pem -text -modulus

解密

1	rsautl -decrypt -inkey private.pem -in flag.enc -out flag

更加具体的细节请参考 openssl --help。

分解整数工具 ¶

网站分解，factor.db
命令行分解，factordb-pycli，借用 factordb 数据库。
yafu

使用：
1. 进入yafu解压目录，打开cmd命令行
2. 输入yafu-x64（即yafu64位文件名）
  命令：factor(n)—— n 为需要分解的大数
若n位数过长,将n值保存在文本文档里，最后一定要有换行符
1
yafu-x64 "factor(@)" -batchfile test.txt
其中test.txt为保存需分解的大质数的文本文档

python库 ¶

primefac ¶

整数分解库，包含了很多整数分解的算法。

gmpy ¶

gmpy.root(a, b)，返回一个元组 (x, y)，其中 x 为 a 开 b 次方的值，y 是判断 x 是否为整数的布尔型变量

gmpy2 ¶

安装时，可能会需要自己另行安装 mpfr 与 mpc 库。

gmpy2.iroot(a, b)，类似于 gmpy.root(a,b)

安装命令：
1
python -m pip install gmpy2

import gmpy2
N = 103461035900816914121390101299049044413950405173712170434161686539878160984549
E = 65537
p = 282164587459512124844245113950593348271
q = 366669102002966856876605669837014229419
L = (p-1)*(q-1)
D = int(gmpy2.invert(E, L)) 
'''
gmpy2.invert()返回值类型为<class 'mpz'>
invert(x,y)  计算 x 关于1模 y 的乘法逆元
'''
enstr = 0xad939ff59f6e70bcbfad406f2494993757eee98b91bc244184a377520d06fc35
destr = gmpy2.powmod(enstr, D, N)
'''
gmpy2.powmod()返回值类型为<class 'mpz'>
gmpy2.powmod(x,y,z)，计算x^y mod z 的值并返回
'''
flag0 = hex(destr)[2:]     # flag0类型为str，存的是十六进制表示的字符串
flag1 = bytes.fromhex(flag0)  # 将其从十六进制转换为byte类型(此时已解释成字符)
flag = str(flag1, 'utf-8')  # 将byte类型转换为str类型
print(flag)

pycrypto ¶

安装
1
sudo pip install pycrypto

使用

import gmpy
from Crypto.Util.number import *
from Crypto.PublicKey import RSA
from Crypto.Cipher import PKCS1_v1_5

msg = 'crypto here'
p = getPrime(128)
q = getPrime(128)
n = p*q
e = getPrime(64)
pubkey = RSA.construct((long(n), long(e)))
privatekey = RSA.construct((long(n), long(e), long(d), long(p), long(q)))
key = PKCS1_v1_5.new(pubkey)
enc = key.encrypt(msg).encode('base64')
key = PKCS1_v1_5.new(privatekey)
msg = key.decrypt(enc.decode('base64'), e)

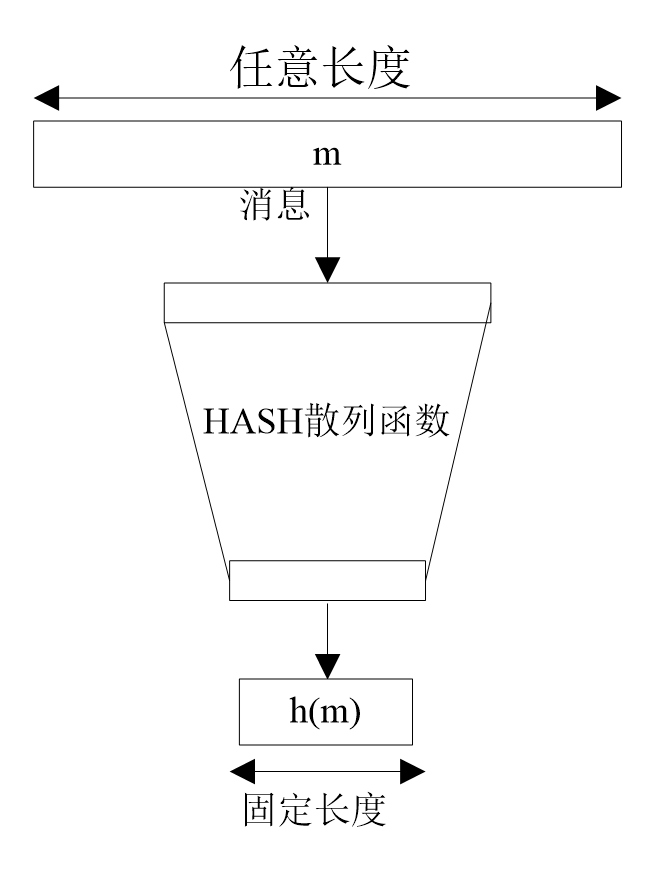
散列算法(哈希函数) ¶

哈希函数（Hash Function）把消息或数据压缩成摘要，使得数据量变小。其一般模型如下图

算法类型	输出 Hash 值长度	是否有常量表
MD5	128 bit / 256 bit
SHA1	160 bit	有
SHA256	256 bit	有
SHA512	512 bit	有

MD5 ¶

MD5 的输入输出如下

输入：任意长的消息，512 比特长的分组。
输出：128 比特的消息摘要。

此外，有时候我们获得到的 md5 是 16 位的，其实那 16 位是 32 位 md5 的长度，是从 32 位 md5 值来的。是将 32 位 md5 去掉前八位，去掉后八位得到的。

特征 ¶

一般来说，我们可以通过函数的初始化来判断是不是 MD5 函数。一般来说，如果一个函数有如下四个初始化的变量，可以猜测该函数为 MD5 函数，因为这是 MD5 函数的初始化 IV。

1	0x67452301，0xEFCDAB89，0x98BADCFE，0x10325476

破解 ¶

目前可以说 md5 已经基本被攻破了，一般的 MD5 的碰撞都可以在如下网上获取到

http://www.cmd5.com/
http://www.ttmd5.com/
http://pmd5.com/
https://www.win.tue.nl/hashclash/fastcoll_v1.0.0.5.exe.zip (生成指定前缀的 md5 碰撞)

SHA1 ¶

SHA1 的输入输出如下

输入：任意长的消息，分为 512 比特长的分组。首先在消息右侧补比特 1，然后再补若干个比特 0，直到消息的比特长度满足对 512 取模后余数是 448，使其与 448 模 512 同余。
输出：160 比特的消息摘要。

一般来说，我们可以通过函数的初始化来判断是不是 SHA1 函数。一般来说，如果一个函数有如下五个初始化的变量，可以猜测该函数为 SHA1 函数，因为这是 SHA1 函数的初始化 IV。

0x67452301
0xEFCDAB89
0x98BADCFE
0x10325476
0xC3D2E1F0

前面四个与 MD5 类似，后面的是新加的。

证书格式解析 ¶

PEM格式证书 ¶

PEM 以 -----BEGIN 开头，以 -----END 结尾，中间包含 ASN.1 格式的数据。ASN.1 是经过 base64 转码的二进制数据。

对RSA的pem证书格式解析 ¶

RSA PEM格式通常为如下两种

PKCS#1格式

1
2
3

-----BEGIN RSA PRIVATE KEY-----
YG6XRKfkcxnaXGfFDWHL....
-----END PRIVATE KEY-----

1
2
3

-----BEGIN RSA PUBLIC KEY-----
YG6XRKfkcxnaXGfFDWHL....
-----END RSA PUBLIC KEY-----

PKCS#8格式

1
2
3

-----BEGIN PRIVATE KEY-----
YG6XRKfkcxnaXGfFDWHL....
-----END PRIVATE KEY-----

1
2
3

-----BEGIN PUBLIC KEY-----
YG6XRKfkcxnaXGfFDWHL....
-----END PRIVATE KEY-----

带有PUBLIC的是RSA的公钥，带有PRIVATE的是RSA的私钥。

PKCS#1格式的密钥头部带有RSA，专指RSA的密钥。

PKCS#8格式的密钥则有可能不是RSA的秘钥，而密钥类型在中间的数据中。

中间的数据是Base64格式的。Base64解码后的二进制数据是.der格式证书的内容。实际上，PEM就是把DER格式的数据用base64编码后，然后再在头尾加上一段“-----”开始的标记而已。

而DER格式是二进制形式，并遵守ASN.1二进制编码格式。^[1]

PKCS#1格式pem解析 ¶

私钥 ¶

首先先利用ius/rsatool: rsatool can be used to calculate RSA and RSA-CRT parameters (github.com)工具生成一个PKCS#1格式的私钥

克隆仓库

1 2	git clone https://github.com/ius/rsatool.git cd rsatool

使用前需安装依赖

1 2	python -m pip install gmpy2 python -m pip install pyasn1

使用命令如下(相应的p、q、e值参考上述例子)

λ python rsatool.py -f PEM -o private1.pem -p 61 -q 53 -e 17
Using (p, q) to calculate RSA paramaters

n = 3233 (0xca1)

e = 17 (0x11)

d = 2753 (0xac1)

p = 61 (0x3d)

q = 53 (0x35)

Saving PEM as private1.pem

这样就在当前目录生成了格式为PKCS#1的RSA私钥文件private1.pem（Base64每76个字符换一行）

1
2
3

-----BEGIN RSA PRIVATE KEY-----
MB0CAQACAgyhAgERAgIKwQIBPQIBNQIBNQIBMQIBJg==
-----END RSA PRIVATE KEY-----

base64解码后得到二进制数据如下：

1	30 1d 02 01 00 02 02 0c a1 02 01 11 02 02 0a c1 02 01 3d 02 01 35 02 01 35 02 01 31 02 01 26

标准的ASN.1编码规则有基本编码规则（BER，Basic Encoding Rules）、唯一编码规则（DER，Distinguished Encoding Rules）等编码规则。而该格式采用的是DER编码，DER编码格式举例详见：DER编码范例

所以上述解码的字符串也可以解释了

30 1d           // RSAPrivateKey, len=0x1d
  02 01 00      // version
  02 02 0c a1   // modulus
  02 01 11      // publicExponent
  02 02 0a c1   // privateExponent
  02 01 3d      // prime1
  02 01 35      // prime2
  02 01 35      // exponent1
  02 01 31      // exponent2
  02 01 26      // coefficient

注意：此处的字节序为大端序

至于内容的格式，可以参考在RFC 2347 RSA私钥ASN.1定义

An RSA private key should be represented with ASN.1 type
RSAPrivateKey:
1
2
3
4
5
6
7
8
9
10
11
12
RSAPrivateKey ::= SEQUENCE {
version Version,
modulus INTEGER, -- n
publicExponent INTEGER, -- e
privateExponent INTEGER, -- d
prime1 INTEGER, -- p
prime2 INTEGER, -- q
exponent1 INTEGER, -- d mod (p-1)
exponent2 INTEGER, -- d mod (q-1)
coefficient INTEGER -- (inverse of q) mod p }

Version ::= INTEGER
The fields of type RSAPrivateKey have the following meanings:

-version is the version number, for compatibility with future
revisions of this document. It shall be 0 for this version of the
document.
-modulus is the modulus n.
-publicExponent is the public exponent e.
-privateExponent is the private exponent d.
-prime1 is the prime factor p of n.
-prime2 is the prime factor q of n.
-exponent1 is d mod (p-1).
-exponent2 is d mod (q-1).
-coefficient is the Chinese Remainder Theorem coefficient q-1 mod p.

也就正如openssl命令解析的一致了

1	openssl rsa -in private1.pem -text -out private1.txt

内容如下

RSA Private-Key: (12 bit, 2 primes)
modulus: 3233 (0xca1)
publicExponent: 17 (0x11)
privateExponent: 2753 (0xac1)
prime1: 61 (0x3d)
prime2: 53 (0x35)
exponent1: 53 (0x35)
exponent2: 49 (0x31)
coefficient: 38 (0x26)
-----BEGIN RSA PRIVATE KEY-----
MB0CAQACAgyhAgERAgIKwQIBPQIBNQIBNQIBMQIBJg==
-----END RSA PRIVATE KEY-----

公钥 ¶

根据上述私钥，生成公钥

1	openssl rsa -in private1.pem -out public1.pem -RSAPublicKey_out

得到公钥文件public1.pem

1
2
3

-----BEGIN RSA PUBLIC KEY-----
MAcCAgyhAgER
-----END RSA PUBLIC KEY-----

Base解码后得到如下，同样是采用DER编码

1
2
3

30 07           // PublicKey,len=7
  02 02 0c a1   // modulus
  02 01 11      // publicExponent

该格式参考的RFC 2347 RSA公钥ASN.1定义

An RSA public key should be represented with the ASN.1 type
RSAPublicKey:
1
2
3
RSAPublicKey::=SEQUENCE{
 modulus INTEGER, -- n
 publicExponent INTEGER -- e }
(This type is specified in X.509 and is retained here for
compatibility.)

The fields of type RSAPublicKey have the following meanings:
-modulus is the modulus n.
-publicExponent is the public exponent e.

相较于私钥，公钥部分较为简单，仅有Modulus(N)和Exponent(e)。

于是我们可以解析出相应的信息如下

1 2	Modulus: 0xca1 Exponent: 0x11

PKCS#8格式pem解析 ¶

私钥 ¶

首先先将上述PKCS#1格式私钥转换为PKCS#8格式

1	openssl pkcs8 -topk8 -inform PEM -in private1.pem -outform pem -nocrypt -out private8.pem

可以得到如下（Base64每64个字符换一行）

-----BEGIN PRIVATE KEY-----
MDMCAQAwDQYJKoZIhvcNAQEBBQAEHzAdAgEAAgIMoQIBEQICCsECAT0CATUCATUC
ATECASY=
-----END PRIVATE KEY-----

参考RFC 5208 - Public-Key Cryptography Standards (PKCS) #8: Private-Key Information Syntax Specification Version 1.2 (ietf.org)

>PrivateKeyInfo ::= SEQUENCE {
>version Version,
>privateKeyAlgorithm AlgorithmIdentifier {{PrivateKeyAlgorithms}},
>privateKey PrivateKey,
>attributes [0] Attributes OPTIONAL }

>Version ::= INTEGER {v1(0)} (v1,...)

>PrivateKey ::= OCTET STRING

>Attributes ::= SET OF Attribute

（同时包含Encrypted private-key information syntax）

可以解析二进制数据位为如下

30 33
  02 01 00      // Version - 0 (v1998)
  30 0d         // AlgorithmIdentifier, len=14
    06 09 2a 86 48 86 f7 0d 01 01 01    // 对于RSA该值固定为1.2.840.113549.1.1.1
    05 00       // NULL(可选参数)
  04 1f             // PrivateKey, len=0x1f
    30 1d           // RSAPrivateKey, len=0x1d
      02 01 00      // version
      02 02 0c a1   // modulus
      02 01 11      // publicExponent
      02 02 0a c1   // privateExponent
      02 01 3d      // prime1
      02 01 35      // prime2
      02 01 35      // exponent1
      02 01 31      // exponent2
      02 01 26      // coefficient

attributes为可选节，这里并没有

同时可以看到RSAPrivateKey部分就是PKCS#1格式中的数据，PKCS#8仅仅是多了些头部描述，因此PKCS#8可以通过不同的AlgorithmIdentifier值(RSA为1.2.840.113549.1.1.1)更加通用的表示其他算法

公钥 ¶

通过openssl生成PKCS#8格式的公钥

1	openssl rsa -in private1.pem -pubout -out public8.pem

得到

1
2
3

-----BEGIN PUBLIC KEY-----
MBswDQYJKoZIhvcNAQEBBQADCgAwBwICDKECARE=
-----END PUBLIC KEY-----

转换格式后

30 1b
  30 0d             // AlgorithmIdentifier, len=14
    06 09 2a 86 48 86 f7 0d 01 01 01  // RSA该值固定为1.2.840.113549.1.1.1
    05 00           // NULL(可选参数)
  03 0a             // PublicKey
    00              // 不知
    30 07           // PublicKey,len=7
      02 02 0c a1   // modulus
      02 01 11      // publicExponent

格式：摘自Cryptographic Interoperability: Keys - CodeProject

>PublicKeyInfo ::= SEQUENCE {
>algorithm AlgorithmIdentifier,
>PublicKey BIT STRING }

>AlgorithmIdentifier ::= SEQUENCE {
>algorithm ALGORITHM.id,
>parameters ALGORITHM.type OPTIONAL }

openssl 相关命令 ¶

rsa命令中

λ openssl rsa -help
Usage: rsa [options]
Valid options are:
 -help              Display this summary
 -inform format     Input format, one of DER PEM
 -outform format    Output format, one of DER PEM PVK
 -in val            Input file
 -out outfile       Output file
 -pubin             Expect a public key in input file
 -pubout            Output a public key
 -passout val       Output file pass phrase source
 -passin val        Input file pass phrase source
 -RSAPublicKey_in   Input is an RSAPublicKey
 -RSAPublicKey_out  Output is an RSAPublicKey
 -noout             Don't print key out
 -text              Print the key in text
 -modulus           Print the RSA key modulus
 -check             Verify key consistency
 -*                 Any supported cipher
 -pvk-strong        Enable 'Strong' PVK encoding level (default)
 -pvk-weak          Enable 'Weak' PVK encoding level
 -pvk-none          Don't enforce PVK encoding
 -engine val        Use engine, possibly a hardware device

openssl rsa -in private1.pem -out public1.pem -RSAPublicKey_out     # 从PKCS#1格式私钥 导出 PKCS#1格式公钥
openssl rsa -in private1.pem -pubout -out public8.pem               # 从PKCS#1格式私钥 导出 PKCS#8格式公钥

openssl rsa -in private8.pem -out private1.pem						# 将PKCS#8格式私钥 转换为 PKCS#1格式私钥
openssl pkcs8 -topk8 -inform PEM -in private1.pem -outform pem -nocrypt -out private8.pem       # 将PKCS#1格式私钥 转换为 PKCS#8格式私钥

openssl rsa -RSAPublicKey_in -in public1.pem -pubout -out public8.pem	# 将PKCS#1格式公钥 转换为 PKCS#8格式公钥
openssl rsa -pubin -in public8.pem -RSAPublicKey_out -out public1.pem	# 将PKCS#8格式公钥 转换为 PKCS#1格式公钥

可以看出

-RSAPublicKey_in 是输入PKCS#1的公钥
-RSAPublicKey_out 是输出PKCS#1的公钥
-pubin 是输入PKCS#8的公钥
-pubout 是输出PKCS#8的公钥

其他 ¶

继续请参考

JAVA实现加解密 ¶

Java加解密环境配置 ¶

SunJCE Provider 支持的Cipher详细信息(部分) — 关于加密数据的填充方式的研究 - 豆丁网 (docin.com)

algorithm(算法)	mode(工作模式)	padding(填充模式)
AES	ECB、CBC、PCBC、CTR、CTS、CFB、CFBB-CFB128等	NoPadding、PKCS5Padding、ISO10126Padding
AESWrap	ECB	NoPadding
ARCFOUR	ECB	NoPadding
Blowfish、DES、DESede、RC2	ECB、CBC、PCBC、CTR、CTS、CFB、CFBB-CFB128等	NoPadding、PKCS5Padding、ISO10126Padding
DESedeWrap	CBC	NoPadding
PBEWithMD5AndDES、PBEWithMD5AndTripleDES、PBEWithSHA1AndDESede、BEWithSHA1AndRC2_40	CBC	PKCS5Padding
RSA	ECB、NONE	NoPadding、PKCS1Padding等

SunJCE 支持	需添加 BouncyCastle 支持
NoPadding
PKCS5Padding	PKCS7Padding
ANSI X923Padding
ISO10126Padding
ISO7816-4Padding
ZeroBytePadding
TBCPadding
	PKCS1Padding

1. 解除java jdk政策限制 ¶

对于Java 8 Update 144和更早版本，需要安装Java密码学扩展（JCE）无限强度管辖权策略文件。
- 相关解除政策限制文件下载 jdk6 | jdk7 | jdk8
- 解压缩后将下载文件中的两个jar替换在%JAVA_HOME%\jre\lib\security下的jar
- 注意：如果您以后决定恢复到原始的受限策略版本，请首先在中备份原始JCE策略文件（US_export_policy.jar和local_policy.jar）$JAVA_HOME/jre/lib/security。
Java 8 Update 151及更高版本
- 包括了“无限强度管辖策略”，但默认情况下不使用。要启用它，您需要java.security在$JAVA_HOME/jre/lib/security（对于JDK）或$JAVA_HOME/lib/security（对于JRE）中编辑java.security文件。取消注释（或包括）该行：
  1
  crypto.policy=unlimited
jdk11

The default JCE policy files bundled in this Java Runtime Environment allow for “unlimited” cryptographic strengths.

For convenience, this software also contains the historic “limited” strength policy files which restricts cryptographic strengths. To use the limited strength policy, instead of the default unlimited policy, you must update the “crypto.policy” Security property (in /conf/security/java.security) to point to the appropriate directory.

You are advised to consult your export/import control counsel or attorney to determine the exact requirements of your location, and what policy settings should be used.

大致意思就是JDK11默认是无限制，可以在$JAVA_HOME/conf/security/java.security文件中配置crypto.policy属性为unlimited或者limited

真tm乱

检测是否已经解除限制 ¶

public static void main(String[] args) {
    try {
        KeyGenerator kg =  KeyGenerator.getInstance("AES");
        kg.init(256);
        SecretKey secretKey=kg.generateKey();
        System.out.println(secretKey.getFormat());
    } catch (NoSuchAlgorithmException e) {
        e.printStackTrace();
    }

}

运行成功则已经解除限制

2.配置BouncyCastle ¶

下载BC：BouncyCastle下载地址

（方法一）全局静态配置 ¶

把bcprov-ext*.jar文件复制到 %JAVA_HOME%\jre\lib\ext 目录下面
修改配置文件\jre\lib\security\java.security

security.provider.1=sun.security.provider.Sun
security.provider.2=sun.security.rsa.SunRsaSign
security.provider.3=sun.security.ec.SunEC
security.provider.4=com.sun.net.ssl.internal.ssl.Provider
security.provider.5=com.sun.crypto.provider.SunJCE
security.provider.6=sun.security.jgss.SunProvider
security.provider.7=com.sun.security.sasl.Provider
security.provider.8=org.jcp.xml.dsig.internal.dom.XMLDSigRI
security.provider.9=sun.security.smartcardio.SunPCSC
security.provider.10=sun.security.mscapi.SunMSCAPI
...

security.provider.11=org.bouncycastle.jce.provider.BouncyCastleProvider

这样添加后便可以启用了，如果IDEA找不到类(无提示)，去【Project Structure】->【Platform Settings】-> 【SDKs】添加相应的jar包路径，或者直接删掉jdk再重新添加。

（方法二）动态添加jar ¶

导入不含ext的另一个jar

所使用的类中添加

1
2
3

static {
    Security.addProvider(new BouncyCastleProvider());
}

验证使用 ¶

public static void main(String[] args) {
    Provider provider = Security.getProvider("BC");
    System.out.println(provider);
    for(Map.Entry<Object,Object> entry:provider.entrySet()){
        System.out.println(entry.getKey()+" --> "+entry.getValue());
    }
}

运行类似下，则配置成功

BC version 1.69
Cipher.ARIARFC3211WRAP --> org.bouncycastle.jcajce.provider.symmetric.ARIA$RFC3211Wrap
Alg.Alias.Cipher.1.3.6.1.4.1.22554.1.1.2.1.22 --> PBEWITHSHAAND192BITAES-CBC-BC
Alg.Alias.AlgorithmParameters.SHA512withRSA/PSS --> PSS
Alg.Alias.Mac.HMAC/Skein-256-224 --> HMACSkein-256-224
Alg.Alias.MessageDigest.SHA256 --> SHA-256

配置CommonsCodec ¶

Commons Codec下载地址

JavaScript实现加解密 ¶

CryptoJS库使用 ¶

下载地址：

GitHub地址：https://github.com/brix/crypto-js
npm下载：npm install crypto-js

使用其中的crypto-js.js文件

更多使用示例参照CryptoJS - CryptoJS (gitbook.io)

解析数据 ¶

// 转为字节数组
var wordArray = CryptoJS.enc.Utf8.parse(utf8String);
var wordArray = CryptoJS.enc.Hex.parse(hexString);
var wordArray = CryptoJS.enc.Base64.parse(base64String);
var wordArray = CryptoJS.enc.Latin1.parse(latin1String);

// 字节数组转
var utf8String = CryptoJS.enc.Utf8.stringify(wordArray);
var hexString = CryptoJS.enc.Hex.stringify(wordArray);
var base64String = CryptoJS.enc.Base64.stringify(wordArray);
var latin1String = CryptoJS.enc.Latin1.stringify(wordArray);

CryptoJS.format.OpenSSL.parse(sslString);
CryptoJS.format.OpenSSL.stringify(wordArray);

MD ¶

MD5 ¶

简单调用 ¶

var hash = CryptoJS.MD5(message);

var hash = CryptoJS.MD5(wordArray);
// MAC
var hmac = CryptoJS.HmacMD5(message, key);

复杂调用 ¶

function md5Example(data) {
    var hasher = CryptoJS.algo.MD5.create();
    hasher.reset(); // 清掉之前设置的明文数据
    hasher.update(data);    // 添加明文数据
    var hash = hasher.finalize();   // 进行加密
    return hash;
}

HmacMD5

function hmacmd5Example(data, key) {
    var hmacHasher = CryptoJS.algo.HMAC.create(CryptoJS.algo.MD5, key);
    hmacHasher.reset(); // 清掉之前设置的明文数据
    hmacHasher.update(data); // 添加明文数据
    var hmac = hmacHasher.finalize(); // 进行加密
    return hmac;
}

SHA ¶

SHA1 ¶

简单调用 ¶

var hash = CryptoJS.SHA1(message);

var hash = CryptoJS.SHA1(wordArray);

// MAC
var hmac = CryptoJS.HmacSHA1(message, key);

SHA224 ¶

简单调用 ¶

var hash = CryptoJS.SHA224(message);

var hash = CryptoJS.SHA224(wordArray);

// MAC
var hmac = CryptoJS.HmacSHA224(message, key);

SHA256 ¶

简单调用 ¶

var hash = CryptoJS.SHA256(message);

var hash = CryptoJS.SHA256(wordArray);

// MAC
var hmac = CryptoJS.HmacSHA256(message, key);

复杂调用 ¶

同md5，将MD5类替换为SHA256即可

SHA3 ¶

格式同上

SHA384 ¶

格式同上

SHA512 ¶

格式同上

DES ¶

示例

function desenExample(data, key) {
    var data = CryptoJS.enc.Utf8.parse(data);
    var key = CryptoJS.enc.Utf8.parse(key);
    var cfg = {
        mode: CryptoJS.mode.ECB, // 加密模式
        padding: CryptoJS.pad.Pkcs7 // 填充方式
    };
    var result = CryptoJS.DES.encrypt(data, // 待加密数据
        key, // 加密密钥
        cfg);
    var restr = result.toString();
    return restr;
}
desenExample("desExample","12345678");

DESede/TripleDES
将上述类名DES换为TripleDES即可

AES ¶

function aesExample(data, key, iv) {
    var key = CryptoJS.enc.Utf8.parse(key);
    var iv = CryptoJS.enc.Utf8.parse(iv);
    var cfg = {
        iv: iv, // iv
        mode: CryptoJS.mode.CBC, // 加密模式
        padding: CryptoJS.pad.Pkcs7
    } // 填充方式
    // format: CryptoJS.format.Hex // 以十六进制输出(默认采用Base64方式)
    var result = CryptoJS.AES.encrypt(data, // 待加密数据
        key, // 加密密钥
        cfg);
    var restr = result.toString();
    return restr;
}

jsencrypt ¶

travist/jsencrypt: A Javascript library to perform OpenSSL RSA Encryption, Decryption, and Key Generation. (github.com)

jsrsasign ¶

kjur/jsrsasign: The ‘jsrsasign’ (RSA-Sign JavaScript Library) is an opensource free cryptography library supporting RSA/RSAPSS/ECDSA/DSA signing/validation, ASN.1, PKCS#1/5/8 private/public key, X.509 certificate, CRL, OCSP, CMS SignedData, TimeStamp, CAdES JSON Web Signature/Token in pure JavaScript. (github.com)

RSA.js ¶

RSA In JavaScript - ohdave.com

在电信和计算机网络领域，ASN.1（Abstract Syntax Notation One) 是一套标准，是描述数据的表示、编码、传输、解码的灵活的记法。它提供了一套正式、无歧义和精确的规则以描述独立于特定计算机硬件的对象结构。ASN.1是一种语言，一种标记语言，作用是描述数据结构。基于这种数据结构可以进行数据的表示、编码、传输和解码。 ↩︎